Welcome to our website scholars.co.tz. In this article, are you looking for TOPIC 1: Numbers – Mathematics Notes Form 1
We know that when we count we start 1,2 …. . But there are other numbers like 0, negative numbers and decimals. All these types of numbers are categorized in different groups like counting numbers, integers, real numbers, whole numbers and rational and irrational numbers according to their properties. all this have been covered in this chapter
Base Ten Numeration
Numbers are represented by symbols called numerals. For example, numeral for the number ten is 10. Numeral for the number hundred is 110 and so on.
The symbols which represent numbers are called digits. For example the number 521 has three (3) digits which are 5, 2 and 1. There are only tendigits which are used to represent any number. These digits are 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.
The Place Value in each Digit in Base Ten Numeration
Identify the place value in each digit in base ten numeration
When we write a number, for example 521, each digit has a different value called place value. The 1 on the right means 1 ones which can be written as 1 × 1, the next number which is 2 means 2 tens which can be written as 2 × 10 and the last number which is 5 means 5 hundreds which can be written as 5 × 100. Therefore the number 521 was found by adding the numbers 5 × 100 + 2 × 10 + 1× 1 = 521.
Natural and Whole Number
Natural numbers are denoted by N. natural numbers can be represented on a horizontal line called number line as shown above:
The Difference between Natural and Whole Numbers
Distinguish between natural and whole numbers
Natural numbers are either used to count one to one objects or represent the position of an object in a sequence. They start from one and go on to infinity.This is why they are sometimes referred to as counting numbers.
The only whole number that cannot be classified as a natural number is 0. Counting numbers can further be classified into perfect numbers, composite numbers, co-prime/ relatively prime numbers, prime numbers, even and odd numbers.
Even ,Odd, and Prime Numbers
Identify even ,odd, and prime numbers
Even numbers are those numbers which are divisible by 2. In other words we can say that any natural number which can be divided by 2 is an even number. For example 2, 4, 6, 8, 10, 12, … are even numbers since they are divisible by 2.
Odd numbers are those numbers which are not divisible by 2. In other words we can say that any natural number when divided by 2 and remains 1 including 1 are called odd numbers. Example 1, 3, 5, 7, 9, 11, 13, 15, … are called odd numbers.
Prime numbers are those numbers which are divisible by one and itself excluding one or any natural number which is divisible by one and itself except one. For example 2, 3, 5, 7, 11, 13, 17, … are called prime numbers.
Odd and Prime Numbers on Numbers Lines
Show even , odd and prime numbers on number lines
Odd and Prime Numbers
Operations with Whole Numbers
We have four operations which are: addition (+), subtraction (-), multiplication ( X) and division (÷).
Addition of Whole Numbers
Add whole numbers
When adding numbers we add the corresponding digits in their corresponding place values and we start adding from the right side i.e. from the place value of ones to the next.
We can add numbers horizontally or vertically.
Horizontal addition
Example 5
- 972 + 18=
- 23 750 + 250 =
- 972 + 18 = 990
- 23 750 + 250 = 24 000
Subtraction of Whole Numbers
Subtract whole numbers
Subtraction is done in similar way like addition. We subtract the corresponding digits in their corresponding place value. For example; 505 – 13. We first subtract ones, which are 5 and 3. Subtract3 from 5 gives 2. Followed by tens which are 0 and 1. Subtract 1 from 0 is not possible. In order to make it easy, take 1 from 5 (hundreds).
When 1 is added to 0 it has to be changed to be tens since it is added to a place of tens. So, when 1 comes into a place of tens it becomes 10. So add 10 to 0. We get 10. Now, subtract 1 from 10. We get 9. We are left with 4 in a place of hundreds since we took 1. There for our answer will be 492.
Note that similar manner will be used when subtracting.
Example 7
Multiplication of Whole Numbers
Multiply whole numbers
Multiplication means adding repeatedly depending on the times number given. For example; 25 6 means add 25, repeat adding 6 times i.e. 25 + 25 + 25 + 25 +25 + 25 = 150. The answer obtained after multiplying two or more numbers is called product. The number being multiplied is called a multiplicand while the number used in multiplying is called a multiplier. Referring our example, 25 is multiplicand and 6 is multiplier.
Example 8
Division of Whole Numbers
Divide whole numbers
Division is the same as subtraction. You subtractdivisor(the number used to divide another number) fromdividend(the number which is to be divided), we repeat subtracting divisor to the answer obtained until we get zero. The answer is how many times you repeat subtraction.
For example; 27 ÷9, we take 27 we subtract 9, we get 18. Again we take 18 we subtract 9, we get 9. We take 9 we subtract 9 we get 0. We repeat subtraction three times. Therefore the answer is 3. The answer obtained is calledquotient. Referring to our example; 27 is dividend, 9 is divisor and 3 is quotient. If a number can’t be divided exactly, what remains or left over is calledremainder.
The Four Operations in Solving Word Problems
Use the four operations in solving word problems
Example 10
- 12 ÷ 4 + 3 x 5
- 14 x2 ÷ 7 – 3 + 6
Solution
- 12 x 4 + 3 x 5 =3 + 15 (do division and multiplication fist) =18
- 14 x 2 ÷ 7 – 3 + 6 =28 ÷ 7 – 3 + 6 (multiply first) =4 – 3 + 6 (then divide) =10 – 3 (add then subtract) =7
Then we do division followed by multiplication, addition and lastly subtraction.
Word problems on whole numbers
Example 12
In a school library there are 6 shelves each with 30 books. How many books are there?
Solution
Each shelf has 30 books
6 shelves have 30 × 6 = 180 books.
Therefore, there are 180 books.
Each row has 25 Cabbages
Therefore in Juma’s mother garden there are 315 plants.
Example 14
A school shop collects sh 90 000 from customers each day. If sh 380 000 from the collection of 6 days was used to buy books. How much money was left?
Each day the collection is sh 90 000
6 days collection is sh 90 000 × 6 = sh 540 000
The money left will be = Total collection – Money used
= sh 540 000 – sh 380 000 = sh 160 000
Therefore the money left was sh 160 000
Exercise 1
- 899 482 (4)
- 1 940 (0)
- 9 123 476
- Ten thousand and fifty one.
- Nine hundred thirty millio
Factors And Multiples Of Numbers
Factors of a Number
Find factors of a number
Consider two numbers 5 and 6, when we multiply these numbers i.e. 5 6 the answer is 30. The numbers 5 and 6 are called factors or divisors of 30 and number 30 is called a multiple of 5 and 6. Therefore factors are the divisors of a number.
Example 15
Find all factors of 12
Note that, when listing the factors we don’t repeat any of it.
Multiples of a Number
Find multiples of a number
Multiples of a number are the products of a number. For example multiples of 4 are 4, 8, 12, 16, 20, 24, … This means multiply 4 by 1, 2, 3, 4, 5, 6, … .
Example 16
Example
List all multiples of 6 between 30 and 45.
Solution
The multiples of 6 are: 6×1 = 6; 6×2 = 12; 6×3 = 18; 6×4 = 24; 6×5 = 30; 6×6 = 36; 6×7 = 42; 6×8 = 48 and so on.
Therefore, multiples of 6 between 30 and 45 are 36 and 42.
Factors to Find the Greatest Common Factors(GCF) of Numbers
Use factors to find the greatest common factors(GCF) of numbers
Greatest Common Factor is sometimes called Highest Common Factor. Its short form is (GCF) or (HCF) respectively. The Greatest Common Factor is the largest common divisor of two or more numbers given.
For example if you are told to find the GCF of 15 and 25. First, list all factors or divisors of 15 and that of 25. Thus, factors of 15 are 1, 3, 5, 15factors of 25 are 1, 5, 25
The common factors are 1 and 5. Therefore the GCF is 5.
Example 17
Example1
Find the HCF of 72 and 120.
Solution
We have to list factors of our numbers:
Factors of 72 are 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Factors of 120 are 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120
Another method which can be used to find the GCF or HCF is prime factorization method.
Example 18
Example
Find the HCF of 36 and 48.
Solution
After writing the numbers as a product of their prime factors, take only the common prime factors (prime factors appeared to all numbers). In our example the common factors are 2×2×3. Therefore the HCF of 36 and 48 is 12.
Lowest Common Multiple (LCM)
Lowest Common Multiple is also called Least Common Multiple and its short form is LCM.For example: multiples of 5 are 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, …multiples of 3 are 3, 9, 15, 18, 21, 24, 27, 30, 33, ….
When you look carefully at these multiples of 5 and 3 you notes that 15 had appeared to both. This multiple which appear to both is called a common multiple. If there are more than one common multiples which appeared the smaller common multiple is what is called Lowest Common Multiple.
Example 19
Find the common multiples and then show the Lowest Common Multiple of the numbers 4, 6 and 8.
Solution
We can find the Lowest Common Multiple (LCM) of numbers by writing the numbers as a product of their prime factors. The method is called prime factorization.
Find the LCM of 24 and 36 by prime factorization method.
Solution
Let us find prime factors of each number by dividing the numbers by their prime factors.
Now take the prime factors which appear to both numbers i.e. 2×2×3 (we take without repeating). We are left with 2 which is a multiple of 24 and 3 which is a multiple 36. We have also to multiply these prime factors left i.e. 2×2×2×3×3. This gives 72. Therefore the LCM of 24 and 36 is 2×2×2×3×3= 72.
Integers
Integers
Consider a number line below
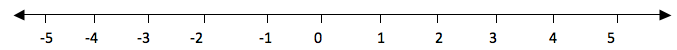
The numbers from 0 to the right are called positive numbers and the numbers from 0 to the left with minus (-) sign are called negative numbers. Therefore all numbers with positive (+) or negative (-) sign are called integers and they are denoted by Ζ.
Numbers with positive sign are written without showing the positive sign. For example +1, +2, +3, … they are written simply as 1, 2, 3, … .
But negative numbers must carry negative sign (-). Therefore integers are all positive and negative numbers including zero (0). Zero is neither positive nor negative number. It is neutral.
The numbers from zero to the right increases their values as the increase. While the numbers from zero to the left decrease their values as they increase. Consider a number line below.
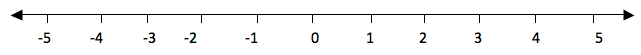
If you take the numbers 2 and 3, 3 is to the right of 2, so 3 is greater than 2. We use the symbol ‘>’ to show that the number is greater than i. e. 3 >2(three is greater than two). And since 2 is to the left of 3, we say that 2 is smaller than 3 i.e. 2<3. The symbol ‘<’ is use to show that the number is less than.
Consider numbers to the left of 0. For example if you take -5 and -3. -5 is to the left of -3, therefore -5 is smaller than -3. -3 is to the right of -5, therefore -3 is greater than -5.
Generally, the number which is to the right of the other number is greater than the number which is to the left of it.
If two numbers are not equal to each to each other, we use the symbol ‘≠’ to show that the two numbers are not equal. The not equal to ‘≠’ is the opposite of is equal to ‘=’.
Example 21
Represent the following integers Ζ on a number line
- 0 is greater than Ζ and Ζ is greater than -4
- -2 is less than Ζ and Ζ is less than or equal to 1.
Solution
a. 0 is greater than Ζ means the integers to the left of zero and Ζ is greater than -4 means integers to the left of -4. These numbers are -1, -2 and -3. Consider number line below
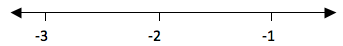
b. -2 is less than Ζ means integers to the right of -2 and Ζ is less than or equal to 1 means integers to the left of 1 including 1. These integers are -1, 0 and 1. Consider the number line below
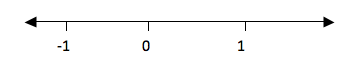
Example 22
Put the signs ‘is greater than’ (>), ‘is less than’ (<), ‘is equal to’ (=) to make a true statement.
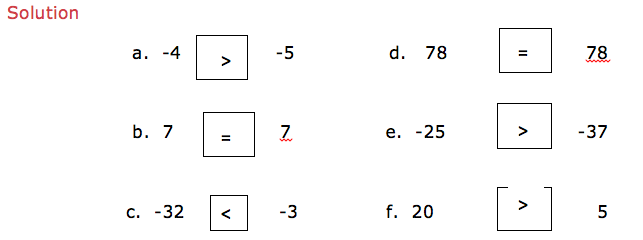
Addition of Integers
Add integers
Example 23
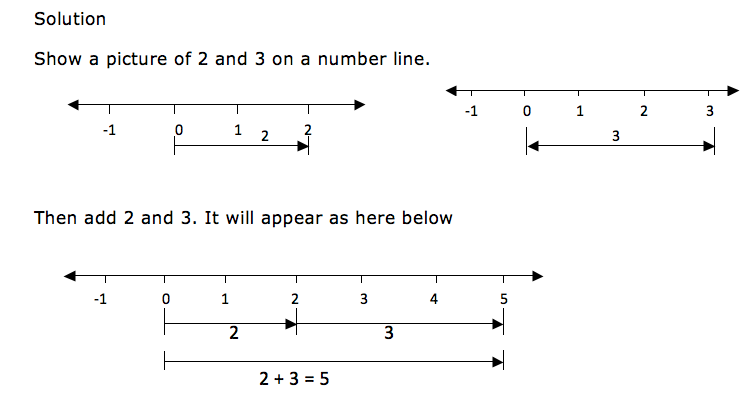
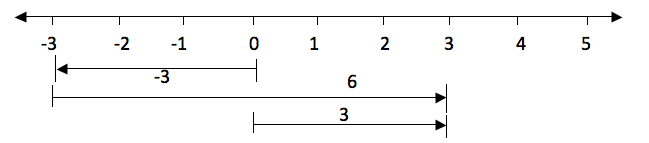
Show a picture of 2 and 3 on a number line.
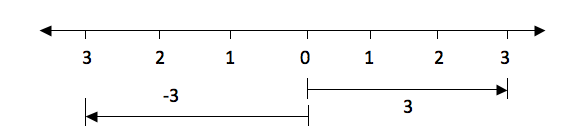
The distance from 0 to 3 is the same as the distance from 0 to -3, only the directions of their arrows differ. The arrow for positive 3 goes to the right while the arrow for the negative 3 goes to the left.
Example 24
Solution
Subtraction of Integers
Subtract integers
Since subtraction is the opposite of addition, if for example you are given 5-4 is the same as 5 + (-4). So if we have to subtract 4 from 5 we can use a number line in the same way as we did in addition. Therefore 5-4 on a number line will be:
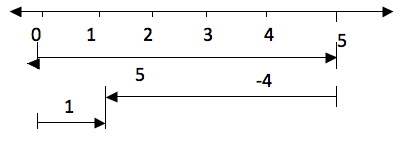
Take five steps from 0 to the right and then four steps to the left from 5. The result is 1.
Multiplication of Integers
Multiply integers
2×6 is the same as add 2 six times i.e. 2×6 = 2 + 2 + 2 + 2 + 2 +2 = 12. On a number line will be:
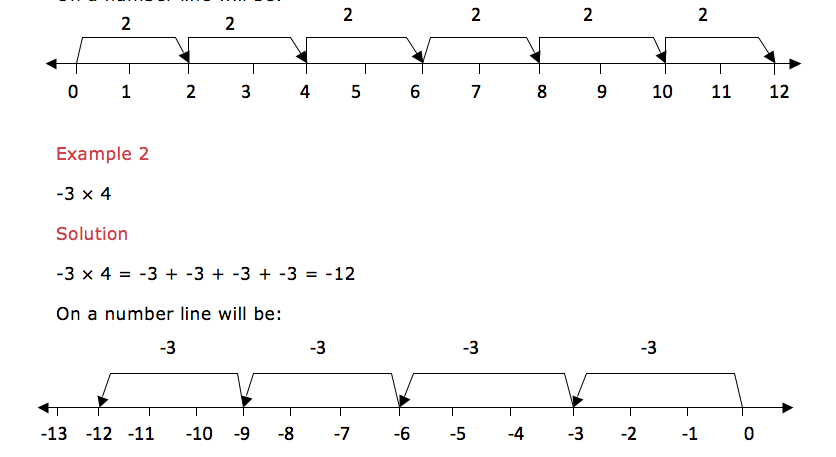
Multiplication of a negative integer by a negative integer cannot be shown on a number line but the product of these two negative integers is a positive integer.
From the above examples we note that multiplication of two positive integers is a positive integer. And multiplication of a positive integer by a negative integer is a negative integer. In summary:
- (+)×,(+) = (+)
- (-)×,(-) = (+)
- (+)×,(-) = (-)
- (-)×,(+) = (-)
Division of Integers
Divide integers
Example 26
6÷3 is the same as saying that, which number when you multiply it by 3 you will get 6, that number is 2, so, 6÷3 = 2.
Therefore division is the opposite of multiplication. From our example 2×3 = 6 and 6÷3 = 2. Thus multiplication and division are opposite to each other.
Dividing two integers which are both positive the quotient (answer) is a positive integer. If they are both negative also the quotient is positive. If one of the integer is positive and the other is negative then the quotient is negative. In summary:
- (+)÷(+) = (+)
- (-)÷(-) = (+)
- (+)÷(-) = (-)
- (-)÷(+) = (-)
Mixed Operations on Integers
Perform mixed operations on integers
You may be given more than one operation on the same problem. Do multiplication and division first and then the rest of the signs. If there are brackets, we first open the brackets and then we do division followed by multiplication, addition and lastly subtraction. In short we call it BODMAS. The same as the one we did on operations on whole numbers.
Example 27
9÷3 + 3×2 -1 =
Solution
9÷3 + 3×2 -1
=3 + 6 -1 (first divide and multiply)
Example 28
(12÷4 -2) + 4 – 7=
(12÷4 -2) + 4 – 7
=5 – 7 (add)
=2
